Diagnostic Tests in Research

Reviewed and revised 15 April 2017

OVERVIEW

Diagnostic tests can be assessed in terms of the following:

• sensitivity
• specificity
• positive predictive value
• negative predictive value
• likelihood ratio (positive or negative)
• receiver operator characteristic curve (ROC curve)

These are based on the following 2×2 table:

Ultimately the quality of a diagnostic test is determined by comparison to the ‘gold standard’ (i.e. the best available alternative)

SENSITIVITY AND SPECIFICITY

Sensitivity

• = ability of a test to detect disease
• = the proportion of disease that was correctly identified
• = true positive rate
• = TP/(TP+FN)

Specificity

• = ability of a test to detect no disease
• = the proportion correctly identified as not having the disease
• = TN/(FP+TN)

Important points about sensitivity and specificity

• not affected by the prevalence of disease
• in order to increase sensitivity the test will become less specific
• sensitivity and specificity looks at the presence and absence of disease to determine the likelihood of the test identifying this correctly
• Remember SNOUT and SPIN: a SeNsitive test rules OUT disease, a SPecific test rules IN disease
• they are of no practical use when it comes to helping the clinician estimate the probability of disease in individual patients as they are defined by the presence or absence of disease and this status is not yet known in our patients (see predictive values below)

False Positive Rate

• = 1 – Specificity
• = FP / (TN + FP)

False Negative Rate

• = 1 – Sensitivity
• = FN / (TP + FN)

POSITIVE AND NEGATIVE PREDICTIVE VALUES

Positive predictive value (PPV)

• = the proportion of a test’s positive results that are truly positive
• = TP/(TP+FP)

Negative predictive value (NPV)

• = the proportion of negative test results that are truly negative
• = TN/(TN+FN)

Important points regarding PPV and NPV

• predictive values take into consideration the prevalence of the disease
• PPV and NPV looks at the subject from the point of view of the test result being positive or negative, and determines the likelihood of it being correct — this is clinically useful
• the usefulness of a test result for an individual patient depends on the prevalence of the disease in the population being tested — a positive result is more useful if there is a higher pre-test probability (in other words, don’t investigate indiscriminately!)
• the same test result may have different predictive values in different settings
• predictive values quoted in the literature may be different to those in your setting, due to differnt pre-test probabilities

LIKELIHOOD RATIOS

Positive Likelihood ratio (aka likelihood ratio for a positive test result)

• = sensitivity / 1 – specificity
• tells us how much MORE likely the patient has the disease if the test is POSITIVE

Negative Likelihood ratio (aka likelihood ratio for a negative test result)

• = (1 – sensitivity) / specificity
• tells us how much LESS likely the patient has the disease if the test is NEGATIVE

Post-test odds

• post-test odds = LR x pre-test odds (according to Bayes Theorem)

Important points regarding Likelihood Ratios

• Likelihood ratios always refer to the likelihood of having disease; the positive and negative designation simply refers to the test result. Hence the interpretation of the post-test odds is always a likelihood of having disease
• Remember that post-test odds are not the same as post-test probabilities!
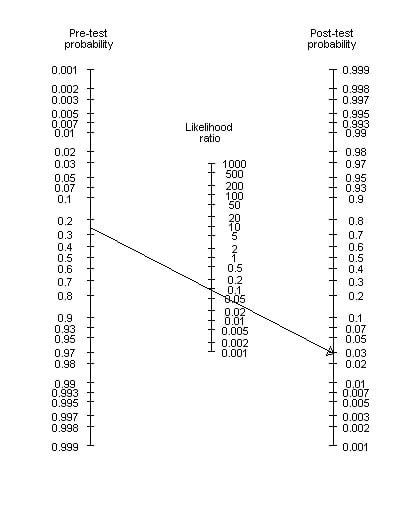
• A Fagan nomogram can be used to determine post-test probability from pre-test probability and likelihood ratios. A Line is drawn from the pre-test probability y-axis through the likelihood ratio y-axis and continued to the post-test probability y-axis to see where it intersects:

RECEIVER OPERATING CHARACTERISTIC (ROC) CURVE

• ROC curves plot sensitivity versus false positive rate for several values of a diagnostic test
• By convention, sensitivity (the proportion of true positive results) is shown on the y axis, going from 0 to 1 (0–100%) and 1-specificity (the proportion of false positive results) is shown on the x axis, going from 0 to 1 (0–100%)
•  illustrates the trade-off between sensitivity and specificity in tests that produce results on a numerical scale, rather than as an absolute positive or negative result

Uses

• determination of the cut-off point at which optimal sensitivity and specificity are achieved
• assessment of the diagnostic accuracy of a test (AUC)
• comparison of the usefulness of two or more diagnostic tests (the more optimal ROC curve is the one connecting the points highest and farthest to the left and has a higher AUC)

Cutoff values

• these are chosen according to whether one wants to maximise the sensitivity (e.g. D-dimer) or specificity (e.g. CTPA) of the test
• e.g. Troponin T levels in the diagnosis of MI
  — several different TNT plasma concentrations would have been chosen and compared against a gold standard in diagnosing MI (ECHO: regional wall abnormalities)
  — the sensitivity and specificity of each chosen TNT level would have been plotted
• the ideal cut off is one which picks up a lot of disease (high sensitivity) but has very few false positives (high specificity)
• one method assumes that the best cut-off point for balancing the sensitivity and specificity of a test is the point on the curve closest to the (0, 1) point, i.e. high up on the left-hand side of the graph resulting in a large AUC method
• an alternative method is to use the Youden index (J), where J is defined as the maximum vertical distance between the ROC curve and the diagonal or chance line

Accuracy and Area-under-the-curve (AUC)

• the higher the AUC, the more accurate test
• AUC = 0.5 means the test is no better than chance alone (plotted as a straight diagonal line)
• AUC = 1.0 means the test has perfect accuracy

ROC slopes and likelihood ratios (see Choi, 1998)

• the tangent at a point on the ROC curve corresponds to the likelihood ratio for a single test value represented by that point
• the slope between the origin and a point on the curve corresponds to the positive likelihood ratio using the point as a criterion for positivity;
• the slope between two points on the curve corresponds to the likelihood ratio for a test result in a defined level bounded by the two points

References and Links

Journal articles

• Akobeng AK. Understanding diagnostic tests 1: sensitivity, specificity and predictive values. Acta Paediatr. 2007 Mar;96(3):338-41. PMID: 17407452. [Free Full Text]
• Akobeng AK. Understanding diagnostic tests 2: likelihood ratios, pre- and post-test probabilities and their use in clinical practice. Acta Paediatr. 2007 Apr;96(4):487-91. PMID: 17306009. [Free Full Text]
• Akobeng AK. Understanding diagnostic tests 3: Receiver operating characteristic curves. Acta Paediatr. 2007 May;96(5):644-7. PMID: 17376185. [Free Full Text]
• Attia J. Moving beyond sensitivity and specificity: using likelihood ratios to help interpret diagnostic tests Aust Prescr 2003;26:111-13 . [Free Full Text]
• Choi BC. Slopes of a receiver operating characteristic curve and likelihood ratios for a diagnostic test. Am J Epidemiol. 1998 Dec 1;148(11):1127-32. PMID: 9850136 [Free Full Text]
• Fan J, Upadhye S, Worster A. Understanding receiver operating characteristic (ROC) curves. CJEM. 2006 Jan;8(1):19-20. PMID: 17175625. [Free Full Text]

FOAM and web resources

• The NNT — Diagnostics and Likelihood Ratios, Explained
• CEBM — Pre-test probability, SpPin and SnNout and Likelihood Ratios
• MedCalc — Bayesian Analysis Model